Series RLC circuit acting as a Resistor, Capacitor and Inductor

Series RLC circuit acting as a Resistor, Capacitor and Inductor 

When a resistor R, capacitor C and inductor L are connected in series with a ac supply voltage, then this circuit is called a series RLC circuit. This circuit can use in three different ways in practical use.

      1.       As inductor
2.      As capacitor and
3.      As resistor

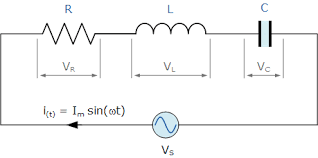Fig-1:  Series RLC circuit

When acts a inductor, RLC circuit will show all the properties of an inductor i.e

1.      This circuit will store energy in  the form of magnetic flux

2.      For ideal case, Phase difference between current and voltage will be 90 degree.

3.      Voltage will lead current by 90 degree.

When acts a capacitor, RLC circuit will show all the properties of an capacitor i.e

1.      This circuit will store energy in  the form of electric charge.

2.      For ideal case, Phase difference between current and voltage will be 90 degree.

3.      Current will lead voltage by 90 degree.

When acts a resistor, RLC circuit will show all the properties of an resistor i.e

1.      This circuit will waste or convert energy in the form of heat.

2.      Phase difference between current and voltage will be zero.

This three different behavior of series RLC circuit will depend on the supply frequency. Besides this three different behavior , this circuit will show another very important phenomenon called resonance, which has extensive used in our daily practical life in electronic circuit.

Total current of a series RLC circuit for a known supply voltage v, Resistance R, Capacitive reactance X_c and Inductive reactance X_L will be

 Current, I = v / sqrt{ R² + (X_L± X_c)² }

Total Impedance of the circuit will be Z =  sqrt{ R² + (X_L± X_c)² }

And Phase difference between voltage and current will be  = tan^-1{(X_L± X_c)/ R }

Now from the equation of impedance , we see that, total impedance of the circuit consists of  resistance , capacitive reactance and inductive reactance and we  know the that

Capacitive reactance X_c = 1 / 2πfC

Inductive reactance , X_L = 2πfL

From these two expression ,we see that, reactance of capacitor and inductor depend on the frequency. If supply frequency increase, capacitive reactance will decrease and inductive reactance will increase but there will be no change in the resistance of the resistor  i.e  resistance is independent on frequency changes.

Inductive Reactance against frequency of a series RLC circuit:

Fig-2: Inductive reactance against frequency in a series RLC circuit

From the graph we see that, inductive reactance increases as the frequency increases. i.e at low frequency inductor shows less impedance but as frequency increases , it shows higher impedance .

Capacitive Reactance against frequency of a series RLC circuit:

Fig-3:  Capacitive reactance against frequency in a series RLC circuit

From the graph we see that,capacitive reactance decreases as the frequency increases. i.e at low frequency capacitor shows high impedance but as frequency increases , it shows low impedance.

Resistance of resistor against frequency of a series RLC circuit:

For resistor, resistance constant. i.e resistance does not depand on the frequency

Total impedance of a series RLC circuit against frequency:

Fig-4: Impedance of a series RLC circuit

Fig-5: Impedance of a series RLC circuit

From the graph, we see that, there are two part in the graph.

1.      Capacitive part ( on the left side of the graph)

2.      Inductive part ( On the right side of  the graph)

When frequency is low, then from the graph we see  that , capacitive reactance is high than the inductive reactance and is still high till a certain frequency f_r .This portion i.e between 0-f_r , is called capacitive part of the circuit. In this part , capacitive reactacne will be higher than the inductive reactance and resistance of RLC circuit  and capacitor reactacne will be dominated and the circuit will act as a capacitor and shows all the properties that a capacitor can show.

When frequency is greater than f_r, inductive reactance will be higher than the capacitive reactance and in this portion i.e ( > f_r) , inductive reactance will dominate and the RLC circuit will act as a inductor and shows all the properties that an inductor can show.

But at f_r,  the capacitive and inductive reactacne will be equal and opposite and in this frequency only resistance of the resistor ( in ideal case) will exit and RLC circuit will act as a resistor and shows all properties that a resistor can show. This frequency is called resonance frequency. At resonance frequency , impedance of the circuit will be minimum and maximum current will flow through the circuit.

At resonance, impedance , Z = R.

Fig-6: Current response of a Series RLC circuit

Topics that will be discussed in details

Electronics, Electrical, Communication
Semiconductor, Diode, Transistor, Field Effect Transistor, Oscillator, Amplifier, Negative Feedback